
Математик-любитель Дэвид Смит продемонстрировал существование эйнштейна — плитки, с помощью которой можно целиком замостить плоскость, и при этом замощение будет только непериодическим. Как следует из препринта работы Смита, она написана в соавторстве с профессиональными математиками Джозефом Самюэлем Майерсом, Крейгом Капланом и Хаимом Гудмэн-Строссом.
Смиту впервые удалось собрать паркет из одной плитки. Фигура, которую придумал математик-любитель, имеет 13 углов и состоит из 16 треугольников с углами 90, 30 и 60 градусов (или из восьми четырехугольников, называемых “воздушными змеями” за сходство с их формой). Плитка Смита по форме напоминает шляпу.
Хитрость “сборки” паркета из “шляпы” состоит в том, что плитки собираются в “суперплитки” все большего размера. Хотя геометрически ни одна “суперплитка” не подобна составляющим ее плиткам, комбинаторно принцип сбора суперплиток на каждом уровне повышения сложности не меняется.
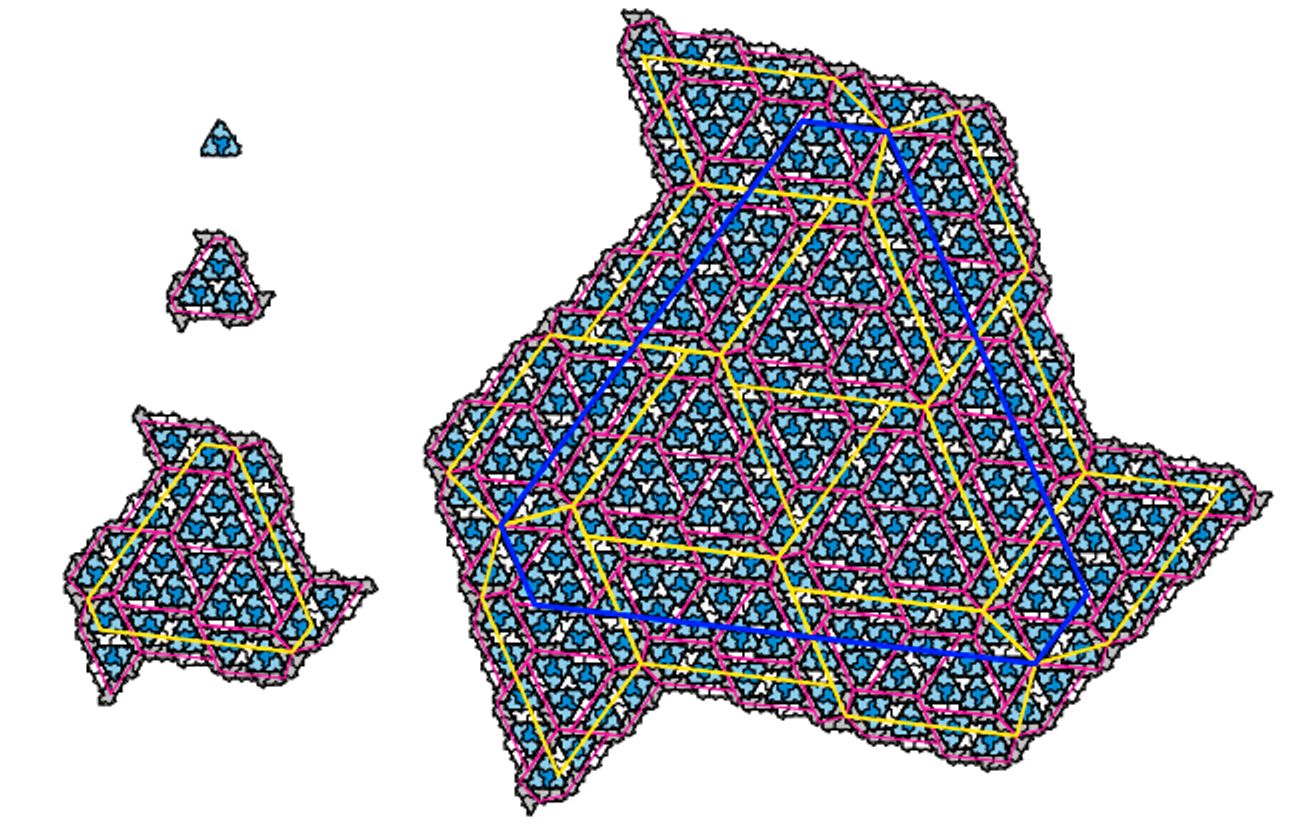
Иллюстрация сбора суперплиток из плиток
Источник: https://arxiv.org/pdf/2303.10798.pdf
Это позволяет авторам доказать, что процесс сбора супер-суперплиток из суперплиток и так далее продолжается неограниченно, поэтому “шляпой” можно замостить всю плоскость, причем такое замощение будет апериодическим. Таким образом, шляпа — это эйнштейн.
Геометров, занимающихся замощениями плоскости, интересует задача Хееша. Числом Хееша фигуры называют максимальное число “слоев” из нее самой, которыми можно окружить эту фигуру. Так, для правильного замощения плоскости число Хееша равно бесконечности. Сам Хееш придумал пример фигуры, копиями которой можно окружить ее саму только один раз.
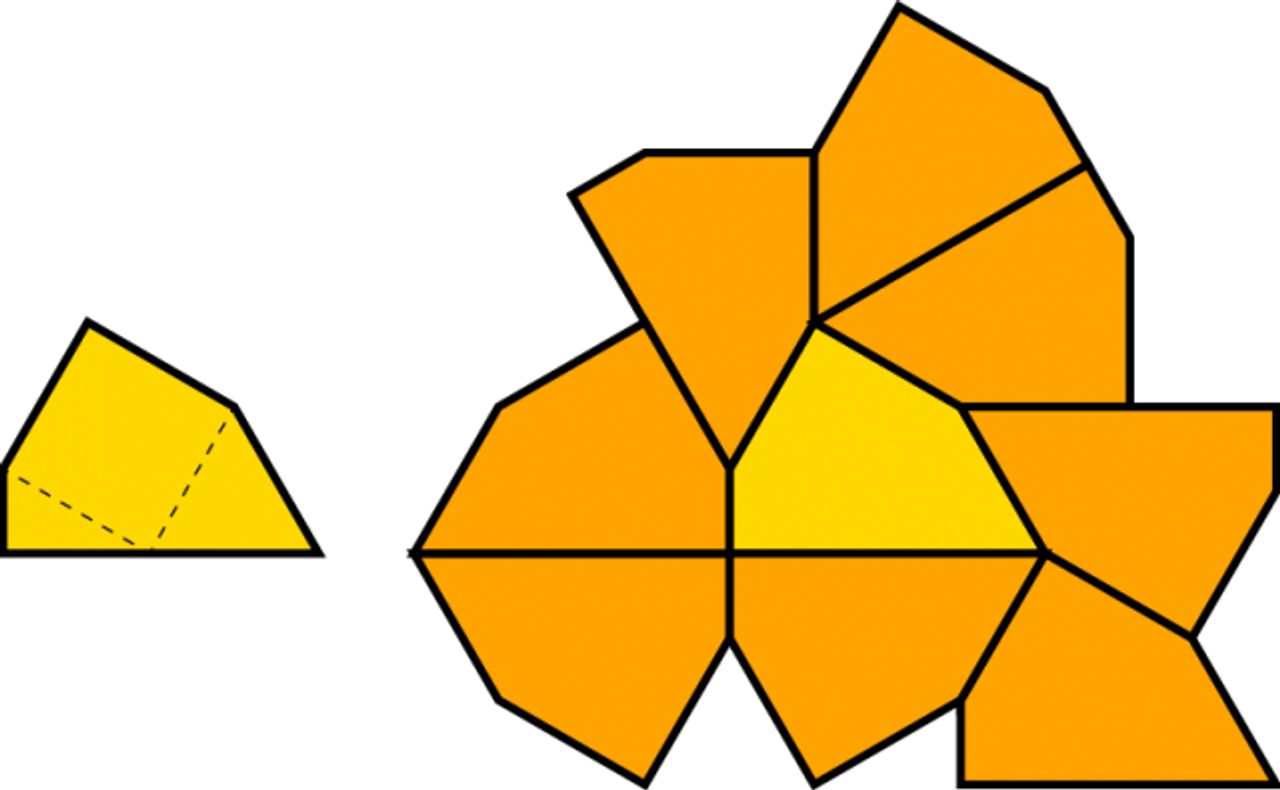
Фигура с числом Хееша 1
Источник: https://isohedral.ca/heesch-numbers-part-1/
В настоящее время известна фигура с максимальным конечным числом Хееша, равным 6.
Фигура с числом Хееша 6
Источник: https://link.springer.com/article/10.1007/s00283-020-10034-w
Задача Хееша состоит в том, чтобы выяснить, фигуры с какими числами Хееша существуют.
Смит был занят тем, что окружал шляпу копиями шляпы. Могло показаться, что в какой-то момент процесс завершится и он найдет фигуру с каким-то числом Хееша. Но процесс не заканчивался, и с помощью программы, написанной Капланом, было установлено, что если бы шляпа не являлась эйнштейном, то ее число Хееша равнялось бы 16. Уже это было бы фантастическим рекордом и крупным достижением. И уже после этого выяснилось, что шляпа может замостить всю плоскость.
Слово «эйнштейн», созвучное с фамилией знаменитого физика, происходит от немецкого “ein Stein”, что в дословном переводе означает “один камень”. Точнее, одна плитка — типа той, которой мостят улицы. Эйнштейном называют такую плитку, что всю плоскость можно замостить ею одной, при этом замощение может быть лишь непериодическим.

Фрагмент замощения плокости "шляпой"
Источник: https://arxiv.org/pdf/2303.10798.pdf
Под периодическим замощением понимают такое замощение, у которого нет двух непараллельных сдвиговых симметрий. Проще говоря, у периодического замощения найдется два направления, при смещении в сторону которых весь рисунок совместится сам с собою.
Этот принцип может быть использован в практических целях. Замощение может быть очень сложным, но если нужно положить кафель в ванной или паркет в гостиной, достаточно будет использовать одинаковые плитки в форме параллелограмма.
Задача на поиск паркетов с заданными свойствами давно привлекала математиков. Так, существует только три замощения плоскости правильными многоугольниками одного сорта. Такие паркеты можно выложить из равносторонних треугольников, квадратов и правильных шестиугольников. Их еще называют “платоновыми паркетами”.
Паркетов, в которых позволено использовать одновременно несколько видов правильных фигур, и при этом они сохраняют высокую степень симметрии (в них любые две вершины связаны преобразованием симметрии, переводящим паркет сам в себя), больше — восемь. Такие паркеты называют архимедовыми.
Можно периодически замостить плоскость любым треугольником и любым четырехугольником. Существуют также 15 пятиугольников, которые позволяют периодически замостить плоскость.
Математики давно хотели показать непериодичные паркеты. В 60-е годы пример такого паркета придумал китайский математик Хао Ван, но чтобы выложить его паркет, потребовалось бы 20 426 видов плиток: все его плитки были квадратными, но различались по цветам ребер, при этом паркет нужно было собирать так, чтобы прилегающие ребра были одного цвета. Затем паркет Вана удалось собрать из 11 типов разноцветных плиток.
Знаменитый математик Роджер Пенроуз сумел собрать непериодический паркет из двух плиток.